함수적 종속성 (Functional Dependency): 한 테이블의 두 속성 집합 간의 제약
함수적 종속성(Functional Dependency, FD)은 한 테이블에 있는 두 개의 속성 집합(set) 사이의 제약을 나타냅니다.
예를 들어, 다음과 같은 컬럼으로 구성된 Employee 테이블이 있다고 가정해봅시다:
| emp_id | emp_name | birth_date | position | salary | dept_id |
이 테이블을 두 개의 속성 집합으로 나눌 수 있습니다:
집합 X
| emp_id |
집합 Y
| emp_name | birth_date | position | salary |
이 두 집합 사이에는 어떤 관계가 있을까요? 이 테이블의 특징은 두 튜플의 X 값이 같다면 Y 값도 같다는 점입니다.
이는 emp_id가 각 직원들을 고유하게 식별하기 위해 만들어진 컬럼이기 때문입니다.
따라서 X 값에 따라 Y 값이 유일하게 결정될 때, 우리는 "X가 Y를 함수적으로 결정한다"고 말합니다.
이러한 두 집합 사이의 제약 관계를 함수적 종속성( X -> Y)이라고 부릅니다.
함수적 종속성(FD)의 파악 방법
함수적 종속성은 테이블의 스키마를 보고 의미적으로 파악해야 합니다.
테이블의 특정 상태를 보고 판단해서는 안 됩니다.
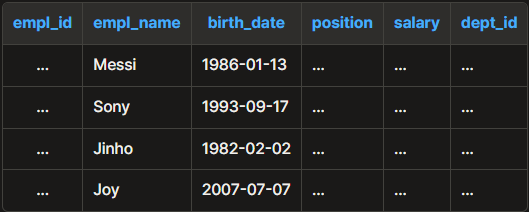
예를 들어, 이 테이블에서 emp_name과 birth_date가 1:1로 매칭된다 해도, 동명이인이 있을 수 있기 때문에 이 사이에 FD가 있다고 보기는 어렵습니다.
따라서 테이블의 스키마를 보고 의미적으로 FD가 존재하는지 파악해야 합니다.
함수적 종속성(FD)의 예시
{stu_id, class_id} -> {grade}
- 학생의 각 수업에서 받은 성적을 저장하는 테이블의 예시
- 여기서 stu_id나 class_id를 유일한 식별자로 FD가 이루어질 수 없는 이유는 학생 하나가 특정 수업에서 받은 성적을 저장하는 테이블이기 때문
{bank_name, bank_account} -> {balance, open_date}
- 은행과 계좌번호에 따라 잔액과 개설일이 결정됨.
- 여기서 bank_account를 유일한 식별자로 FD가 이루어질 수 없는 이유는 다른 종류의 은행에 동일한 계좌번호가 존재할 수 있기 때문
FD의 비대칭성
X -> Y가 성립된다고 해서 Y -> X가 성립하는 것은 아닙니다.
예를 들어, emp_id -> emp_name은 FD이지만, emp_name -> emp_id는 FD가 될 수 없습니다. 왜냐하면 동명이인이 존재할 수 있기 때문입니다.
자명한 함수적 종속성(Trivial Functional Dependency)
X -> Y가 FD로 성립할 때, Y가 X의 부분집합인 경우 자명한 함수적 종속성(Trivial FD)이라고 합니다.
예를 들어, {a, b, c} -> {b, c,}는 자명한 FD입니다.
비자명한 함수적 종속성(Non-Trivial Functional Dependency)
Y가 X의 부분집합이 아닌 경우를 비자명한 함수적 종속성(Non-Trivial FD)이라고 합니다.
예를 들어, {a, b, c} -> {b, c, d}는 비자명한 FD입니다.
부분 함수적 종속성(Partial Functional Dependency)
X -> Y가 FD로 존재할 때,
X 집합의 어떤 진부분집합(proper subset)이라도 Y를 결정지을 수 있다면,
이 때 X -> Y는 부분 함수적 종속성(Partial FD)입니다.
예를 들어, {emp_id, emp_name} -> {birth_date}가 FD일 때,
사실 emp_id 하나만으로 birth_date를 결정지을 수 있기 때문에, {emp_id, emp_name} -> {birth_date}는 부분 FD입니다.
출처
'DB' 카테고리의 다른 글
| [Database] B tree가 데이터베이스 인덱스로 사용되는 이유 (1) | 2024.06.12 |
|---|---|
| [Database] 함수적 종속성을 활용한 테이블 정규화 과정 (0) | 2024.06.10 |
| PostgreSQL, MySQL 에서의 Lost update 대처 방안 (0) | 2024.06.06 |
| RDBMS에서의 MVCC(MutliVersion Concurrency Control) 도입 배경과 원리 + 예제 (1) | 2024.06.06 |
| 트랜잭션 격리 수준 'read committed' 에서의 lost update 해결 (1) | 2024.06.03 |
